Konsep Persamaan Nilai Mutlak

Dari sudut pandang geometri, nilai mutlak dari x ditulis | x |, adalah jarak dari x ke 0 pada garis bilangan real. Karena jarak selalu positif atau nol maka nilai mutlak x juga selalu bernilai positif atau nol untuk setiap x bilangan real.

Secara formal, nilai mutlak x didefinisikan dengan |x|={−x jika x ≥ 0 atau –x jika x < 0 atau dapat pula ditulis :

Contoh 1
Tentukan himpunan penyelesaian dari |2x – 7| = 3

Jawab :
Berdasarkan sifat a :
|2x – 7| = 3  ⇔  2x – 7 = 3  atau  2x – 7 = -3
|2x – 7| = 3  ⇔  2x = 10  atau  2x = 4
|2x – 7| = 3  ⇔  x = 5  atau  x = 2

Jadi, HP = {2, 5}.

Contoh 2
Tentukan HP dari |2x – 1| = |x + 4|

Jawab :
Berdasarkan sifat a :
|2x – 1| = |x + 4|

⇔  2x – 1 = x + 4  atau  2x – 1 = -(x + 4)
⇔  x = 5  atau  3x = -3
⇔  x = 5  atau  x = -1

Jadi, HP = {-1, 5}.

Contoh 3

Tentukan himpunan penyelesaian dari |4x + 2| ≥ 6

Jawab :
Berdasarkan sifat c :
|4x + 2| ≥ 6  ⇔  4x + 2 ≤ -6  atau  4x + 2 ≥ 6
|4x + 2| ≥ 6  ⇔  4x ≤ -8  atau  4x ≥ 4

|4x + 2| ≥ 6  ⇔  x ≤ -2  atau  x ≥ 1

Jadi, HP = {x ≤ -2  atau  x ≥ 1}.

Contoh 4

Tentukan HP dari 2 < |x – 1| < 4

Jawab :
Ingat : a < x < b  ⇔  x > a  dan  x < b

Jadi, pertaksamaan 2 < |x – 1| < 4 ekuivalen dengan
|x – 1| > 2  dan  |x – 1| < 4

Berdasarkan sifat c :
|x – 1| > 2  ⇔  x – 1 < -2  atau  x – 1 > 2
|x – 1| > 2  ⇔  x < -1  atau  x > 3   …………….(1)

Berdasarkan sifat b :
|x – 1| < 4  ⇔  -4 < x – 1 < 4
|x – 1| < 4  ⇔  -3 < x < 5   ……………………….(2)

Irisan dari (1) dan (2) diperlihatkan oleh garis bilangan berikut

Jadi, HP = {-3 < x < -1  atau  3 < x < 5}

Dibawah ini ada beberapa soal yang dapat Anda coba kerjakan 

1. Himpunan penyelesaian dari |2x + 3| = 9 adalah… .

Pembahasan:

2. Jika |x + 1| + 2x = 7, maka nilai x yang memenuhi adalah … .

Pembahasan:

3. Nilai x yang memenuhi persamaan |2x−6| = −2 adalah… .

Pembahasan:

4. Himpunan penyelesaian dari |4x – 2| = |x + 7| adalah… .

Pembahasan:

5. Nilai x yang memenuhi |3x − 6|−|x + 2| = 0 adalah… .

Pembahasan 

6. Himpunan penyelesaian dari |+7/2−1| = 2 adalah… .

Pembahasan:

7. Tentukan nilai x yang memenuhi persamaan |2x – 5| = 3 + 2 |7 – x|.

Pembahasan:

8. Himpunan penyelesaian dari |+7/2−1| = 2 adalah… .

Pembahasan:

Sistem Persamaan Linier Dua Variabel

Persamaan Linear Dua Variabel (PLDV) adalah sebuah bentuk relasi sama dengan pada bentuk aljabar yang memiliki dua variabel dan keduanya berpangkat satu. Dikatakan Persamaan Linear karena pada bentuk persamaan ini jika digambarkan dalam bentuk grafik, maka akan terbentuk sebuah grafik garis lurus (linear).

Bentuk Umum Sistem Persamaan Linear Dua Variabel (SPLDV)

Bagaimana, sudah paham kan letak perbedaannya? Apabila terdapat dua atau lebih PLDV yang memiliki hubungan satu sama lain dan memiliki satu buah penyelesaian, maka itulah yang dinamakan dengan SPLDV. Bentuk umum SPLDV adalah sebagai berikut:

Ada beberapa metode untuk menyelesaikan SPLDV sehingga diperoleh nilai himpunan penyelesaiannya yaitu metode grafik, metode eliminasi dengan penyamaan, metode eliminasi dengan substitusi, dan metode eliminasi dengan menjumlahkan atau mengurangkan. Setiap metode mempunyai keunggulan dan kelemahannya. Penjelasannya setiap metode SPLDV adalah sebagai berikut : 

1. Metode Grafik 

Metode grafik adalah menentukan titik potong antara dua persamaan garis sehingga di dapatkan himpunan penyelesaian dari persamaan linear dua variabel tersebut. Apabila diperoleh persamaan dua garis tersebut saling sejajar, maka himpunan penyelesaiannya adalah himpunan kosong. Sedangkan jika garisnya saling berhimpit maka jumlah himpunan penyelesaiannya tak berhingga. Langkah-langkah penyelesaian menggunakan metode grafik adalah sebagai berikut : 

1. Gambarkan grafik garis ax + by = p dan cx + dy = q pada sebuah sistem koordinat Cartesius. Pada langkah ini, kita harus menentukan titik potong sumbu X dan titik potong sumbu Y nya yaitu titik potong sumbu X saat y = 0 dan titik potong sumbu Y saat x = 0. Lalu kemudian hubungan kedua titik potong tersebut sehingga diperoleh garis persamaan.
2. Tentukan koordinat titik potong kedua garis ax + by = p dan cx + dy = q (jika ada).
3. Tuliskan himpunan penyelesainnya.

Contoh soal :
Tentukan himpunan penyelesaian dibawah ini menggunakan metode grafik.

2x – y = 2

x + y = 4

Pembahasan : 

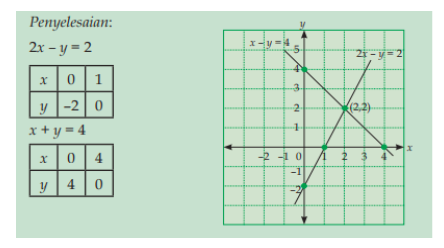
Titik potong kedua garis yang diperoleh adalah (2,2). Jadi himpunan penyelesaiannya dari sistem persamaan tersebut adalah (2,2).

Contoh soal :

Tentukan himpunan penyelesaian dari sistem di bawah ini menggunakan metode grafik : 

x – y = 2

2x – 2y = -4

Pembahasan : 

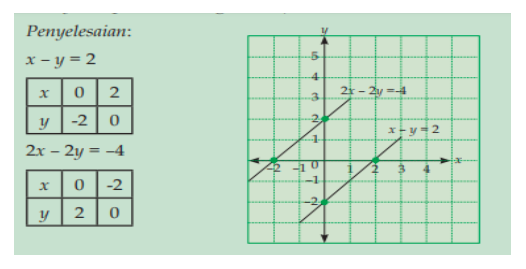
Kedua garis yang dihasilkan ternyata saling sejajar, oleh sebab itu tidak ada titik potong yang di hasilkan. Jadi himpunan penyelesaiannya adalah himpunan kosong {  } . 

Contoh soal :

Tentukan himpunan penyelesaian dari sistem persamaan di bawah ini menggunakan metode grafik : 

x – y = -2

2x – 2y = -4

Pembahasan : 

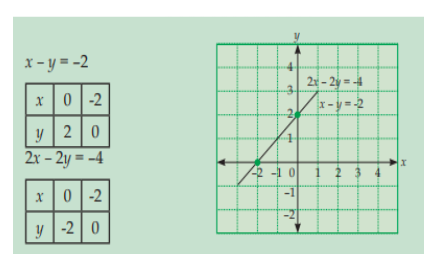
Kedua garis yang dihasilkan ternyata saling berimpit. Maka himpunan penyelesaian dari sistem persamaan linear dua variabel tersebut tak berhingga banyaknya. 

Keunggulan dari metode grafik adalah kita dapat menentukan himpunan penyelesaiannya secara visual. Artinya hasilnya dapat diketahui secara langsung sekali lihat. Kelemahan dari metode grafik adalah tidak efektif untuk menyelesaikan soal untuk aplikasi SPLDV, tidak baik apabila angka yang ada pada persamaan linear dua variabel berbentuk desimal karena kelihatan tidak presisi pada media grafiknya. 

2. Metode Eliminasi dengan Penyamaan

Misalkan kita mempunyai SPLDV dalam variabel x dan y. Andaikan kita membuat suatu persamaan yang tidak lagi mengandung nilai x nya, maka dikatakan bahwa x telah dieliminasikan dengan penyamaan. Langkah strateginya adalah dengan mencari nilai x dari kedua persamaan yang diberikan itu (nilai y seolah-olah dianggap sebagai bilangan yang diketahui, maka dikatakan bahwa x dinyatakan dalam y). Kemudian hasil yang didapat dipersamakan. Dalam kasus ini kita juga dapat menyatakan nilai y ke dalam x, kemudian kita samakan dari persamaan-persamaan itu. Contohnya sebagai berikut : 

Carilah himpunan penyelesaian dari SPLDV berikut ini : 

3x + 5y = 21

2x – 7y = 45

Penyelesaian : 

Jadi, Himpunan Penyelesaiannya adalah {12,-3}.

Kelemahan dari metode eliminasi dengan penyamaan adalah akan memerlukan banyak langkah (dapat sampai 4 langkah), karena misalnya salah satu variabel yang diketahui tidak langsung disubstitusi ke persamaan, namun dicari variabel yang lain menggunakan eliminasi sehingga rawan akan ketidaktelitian saat menghitung. 

3. Metode Eliminasi dengan Substitusi

Apabila kita mempunyai SPLDV dalam variabel x dan y. langkah-langkah penyelesaian metode Eliminasi dengan Substitusi adalah sebagai berikut : 

1. Pilihlah salah satu persamaan yang sederhana, kemudian nyatakan y dalam x atau x dalam y.
2. Substitusikan x atau y yang diperoleh pada langkah 1 ke dalam persamaan lainnya.
3. Selesaikan persamaan yang diperoleh pada langkah 2.
4. Tuliskan himpunan penyelesainnya.

Contoh soal: Metode Eliminasi dengan Substitusi
Carilah himpunan penyelesaian dari SPLDV berikut ini : 

3x + 2y = 10

9x – 7y = 43

Penyelesaian : 

Langkah 1 : nyatakan ke dalam variabel y

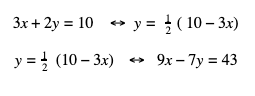
Langkah 2 : selesaikan nilai x dan y

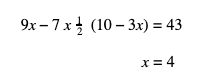
Langkah 3 : substitusikan nilai x dan y ke dalam persamaan : 

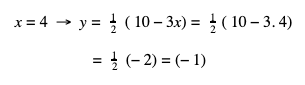
Jadi, Himpunan penyelesaiannya adalah {4, -1}.

Keunggulan Metode Eliminasi dengan Substitusi adalah sangat mudah digunakan dan efektif untuk menyelesaikan soal SPLDV secara cepat dan tepat. Kelemahan dari metode ini adalah tidak disarankan apabila digunakan untuk masalah persamaan linear yang kompleks seperti sistem persamaan linear 3 variabel.

4. Metode Gabungan Eliminasi Menjumlahkan atau mengurangkan dan Substitusi

Apabila kita mempunyai Sistem Persamaan linear dua variabel ke dalam variabel x dan y. langkah-langkah untuk menyelesaikan SPLDV ini adalah sebagai berikut : 

Langkah 1 : Tentukan nilai x atau y menggunakan metode eliminasi dengan menjumlahkan atau mengurangkan.

Langkah 2 : Substitusikan nilai x atau y yang diperoleh pada langkah 1 ke salah satu persamaan yang diperoleh dan selesaikanlah persamaan itu.

Langkah 3 : Tulislah himpunan penyelesaiannya.

Contoh soal : 

Carilah Himpunan penyelesaian dari SPLDV berikut ini :

4 (x-1) + y = 5x – 3y + 6

3x – 2y – 4 = 2x + 2

Penyelesaian : 

Jabarkan persamaan di atas terlebih dahulu sehingga didapat persamaan yang sederhana : 

4 (x-1) + y = 5x – 3y + 6

    4x – 4 + y = 5x – 3y + 6

x – 4y = -10…………………….(1)

3x – 2y – 4 = 2x + 2

   3x – 2y + 4 = 2x + 2

x – 2y = -2 …………………. (2)

Langkah 1 : Tentukan nilai x dan y menggunakan metode eliminasi dan substitusi : 

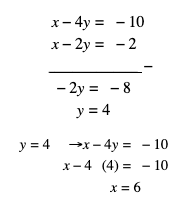
Jadi, himpunan penyelesaiannya adalah {6,-2}.

Berikut ini ada beberapa soal yang dapat Anda coba kerjakan 

1. Nilai p, yang memenuhi persamaan 4p + 3q = 20  dan 2p – q = 3 adalah…

Pembahasan

2. Nilai x dan y berturut-turut yang memenuhi persaman x + 5y = 13 dan 2x – y = 4 adalah…

Pembahasan : 

3. Himpunan penyelesaian dari sistem persamaan 2x + xy = 4 dan 3x + y =6 adalah:

Pembahasan : 

4. Harga 8 buah buku tulis dan 6 buah pensil Rp. 14.400,00 harga 6 buah buku tulis dan 5 buah pensil Rp. 11.200,00. Jumlah harga 5 buah buku tulis dan 8 buah pensil adalah…

Pembahasan : 

5. Penyelesaian dari sistem persamaan 3x + 5y = – 9 dan 5x + 7y = – 19 adalah x dan y. Nilai 4x + 3y adalah… 

Pembahasan : 

6. Umur Sani 7 tahun lebih tua dari umur Ari. Sedangkan jumlah umur mereka adalah 43 tahun. Berapakah umur masing-masing …

Pembahasan : 

7. Harga 2 kg salak dan 3 kg jeruk adalah RP.32.000,00, sedangkan harga 3 kg salak dan 2 kg jeruk adalah RP.33.000,00. Harga 1 kg salak dan 5 kg jeruk adalah…

Pembahasan : 

8. Berapakah nilai 6x – 2y jika x dan y merupakan penyelesaian dari system persamaan 3x + 3y = 3 dan 2x – 4y  = 14  adalah…

Pembahasan : 

9. Nilai x dan y yang memenuhi persamaan linier 2x + y = 6, dan 2x +4y = 9 adalah… 

Pembahasan : 

10. Andi membeli 1 pulpen dan 1 buku dengan harga Rp 2000,- di toko yang sama Budi membeli 5 pulpen dan 2 buku dengan harga Rp 7000,- . berapakah harga 1 buah pilpen?

Pembahasan :